 |
1. 薄膜褶皱演化分析的参变量变分原理(PVP)和大变形分析有限元方法
柔性张拉薄膜在航天工程中广泛使用,如太阳帆、太阳翼和反射天线等(图1)。而充气薄膜由于具有轻质、可折叠、易展开等特点,而备受航天工程师的青睐,已得到的应用包括太阳帆充气桅杆、柔性充气太空舱等。作为薄膜结构常见的失稳变形模式,褶皱往往对结构功能产生不利影响。褶皱的产生属于屈曲问题,而其演化过程则可视为后屈曲。后屈曲问题的平衡路径由于存在分岔点和“Snap back”等现象,非线性程度高,进而给有限元分析造成求解困难,也就无法对薄膜结构进行高效的无褶设计。
课题组基于张力场理论,建立了薄膜结构褶皱变形的无压缩材料模型;从变分原理源头出发,推导并证明了无压缩、无拉伸材料非线性分析的统一参变量势能原理和余能原理。在此基础上,提出能够准确模拟薄膜褶皱演化过程(图2左)的互补有限元方法。对屈服函数的线性化处理,将原非线性问题被转化为系列线性互补方程进行求解,从而避免了常规牛顿类迭代方法在分析无拉伸(无压缩)材料时的不收敛问题。该方法可应用于薄膜结构的无褶设计(图2右)。进一步结合共旋有限元方法,将该方法(PVP-CR)成功地应用到方形气囊(图3)等典型充气结构的承载大变形分析,数值模拟结果与实验测试吻合良好,能够准确预测局部褶皱区域和结构承载极限。

图1.可展开柔性薄膜太阳帆
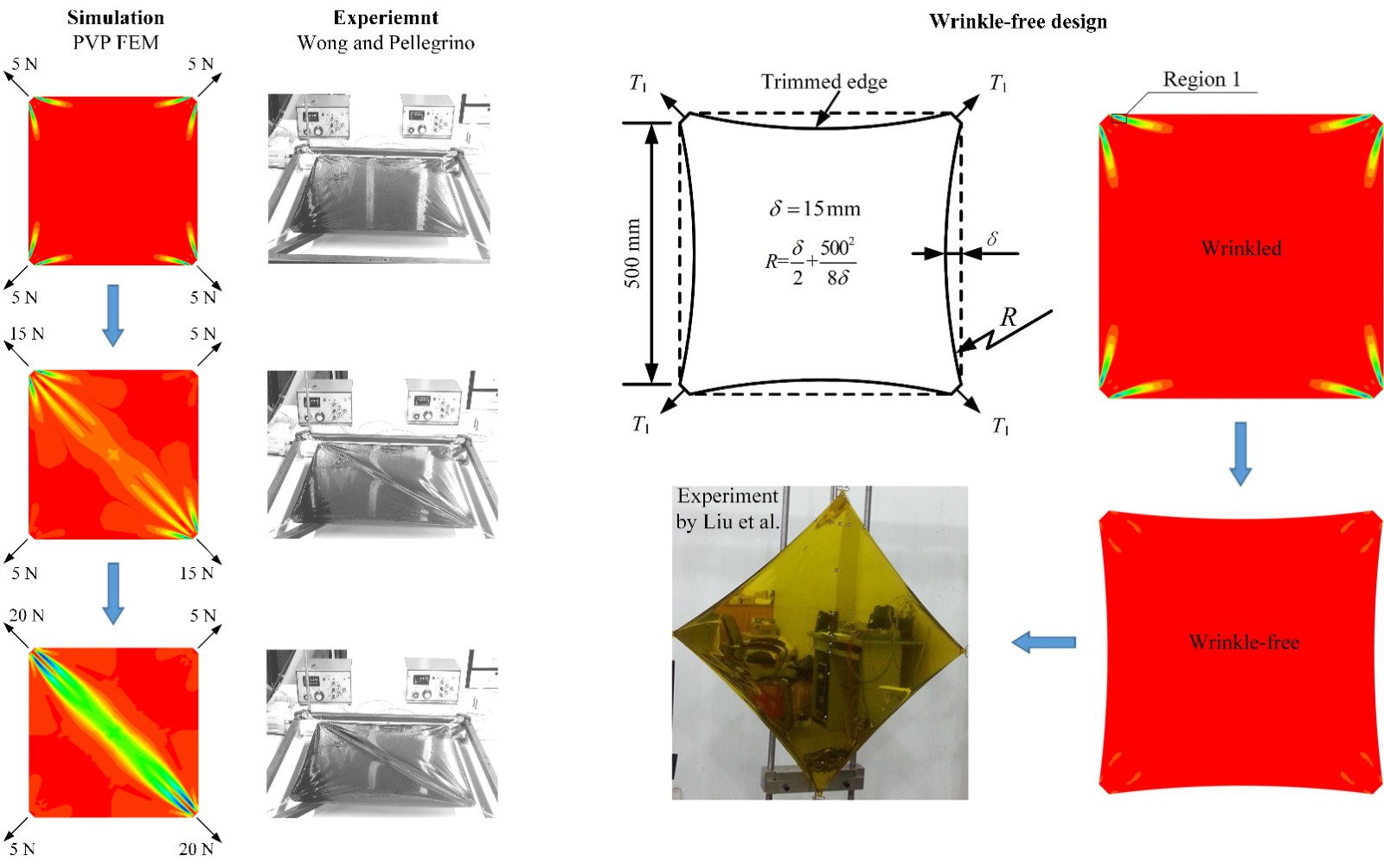
图2.方膜对角拉伸数值模拟与无褶设计
[相关论文]
Mengkai Lu, Liang Zhang*, Xingjie Chen, Anatoly Vershinin, Variational formulations of no-tension/compression solids and the applications to masonry and wrinkled membrane, International Journal of Solids and Structures, 2023, 275: 112298.
https://doi.org/10.1016/j.ijsolstr.2023.112298

图3.方形气囊充气大变形模拟与实验验证
[相关论文]
Zhang L*, Dong KJ, Lu MK, Zhang HW, A wrinkling model for pneumatic membranes and the complementarity computational framework, Computational Mechanics, 2020, 65(1): 119-134.
https://doi.org/10.1007/s00466-019-01755-7
Zhang L, Gao Q, Zhang HW*, Analysis of 2-D bimodular materials and wrinkled membranes based on the parametric variational principle and co-rotational approach, International Journal for Numerical Methods in Engineering, 2014, 98(10): 721-746.
https://onlinelibrary.wiley.com/doi/10.1002/nme.4649
2.基于数据驱动的张拉整体机器人步态设计
基于张拉整体的软机器人和柔性臂因其轻量、低成本和强大的环境适应性而在过去十年中引起了广泛的研究兴趣。然而,有效的驱动方法仍然需要深入研究,另一个关键问题是如何纠正模拟与实物模型之间不可避免的差异。课题组提出了一种创新的杆件屈曲驱动方式,这一方法能够显著减少作动器的数量并提高整体系统的抗冲击性。
课题组采用数据驱动的“混合孪生”方法,增强了贪婪搜索算法生成步态规划的能力。为了进行比较,制作了两个张拉整体机器人的原型,一个采用杆件屈曲驱动,另一个采用绳索收缩驱动。通过运动捕捉系统(MCS)和高速摄像机进行的行走和冲击试验揭示了杆件屈曲驱动结构在自身重量和抗冲击性方面的可行性和优势(图4、图5)。杆件屈曲驱动的概念可以在基于张拉整体结构的连续臂中找到更多的应用,特别是在需要减振或隔离功能的领域。
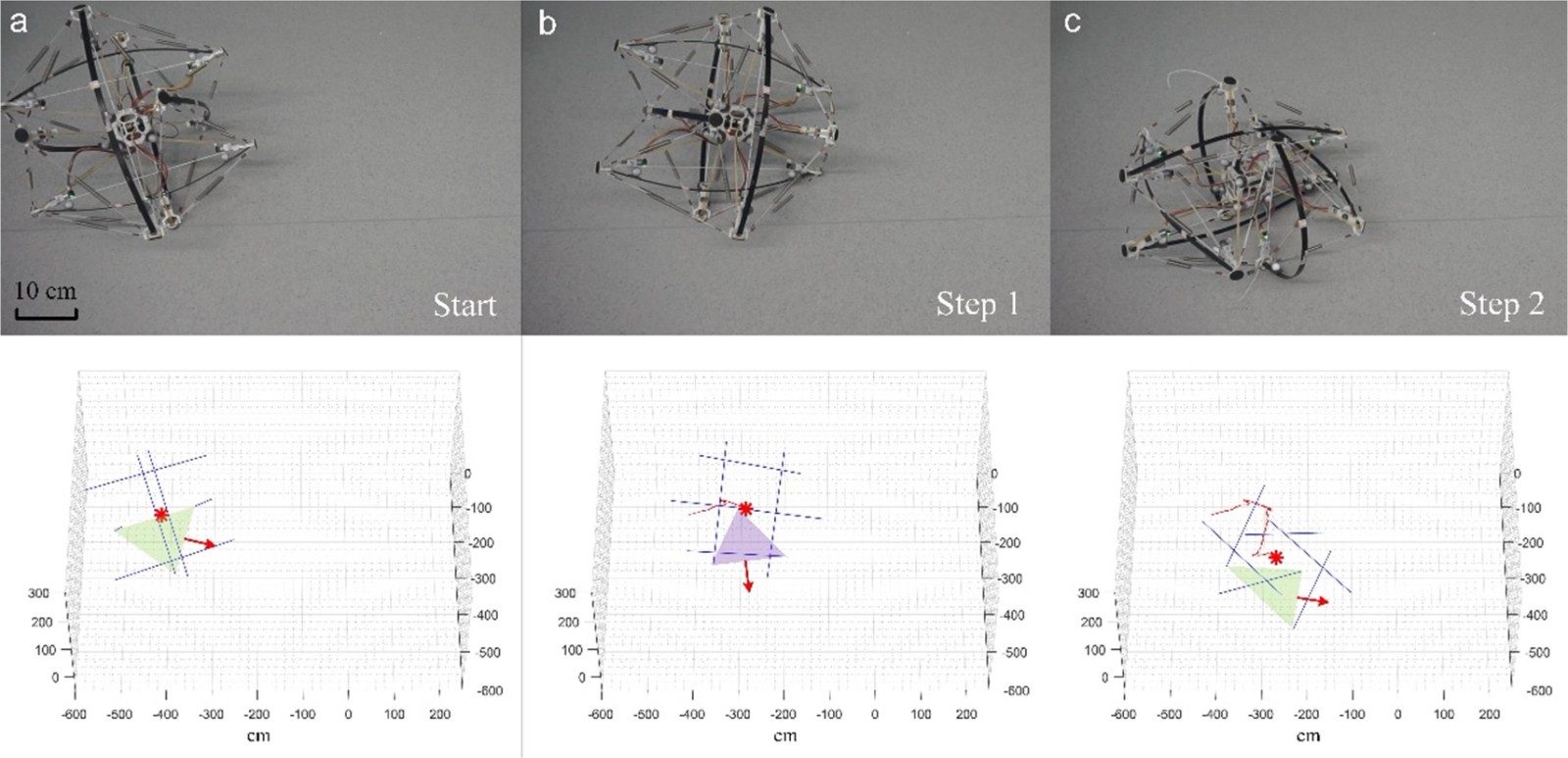
图4.张拉整体机器人行走瞬时摄影
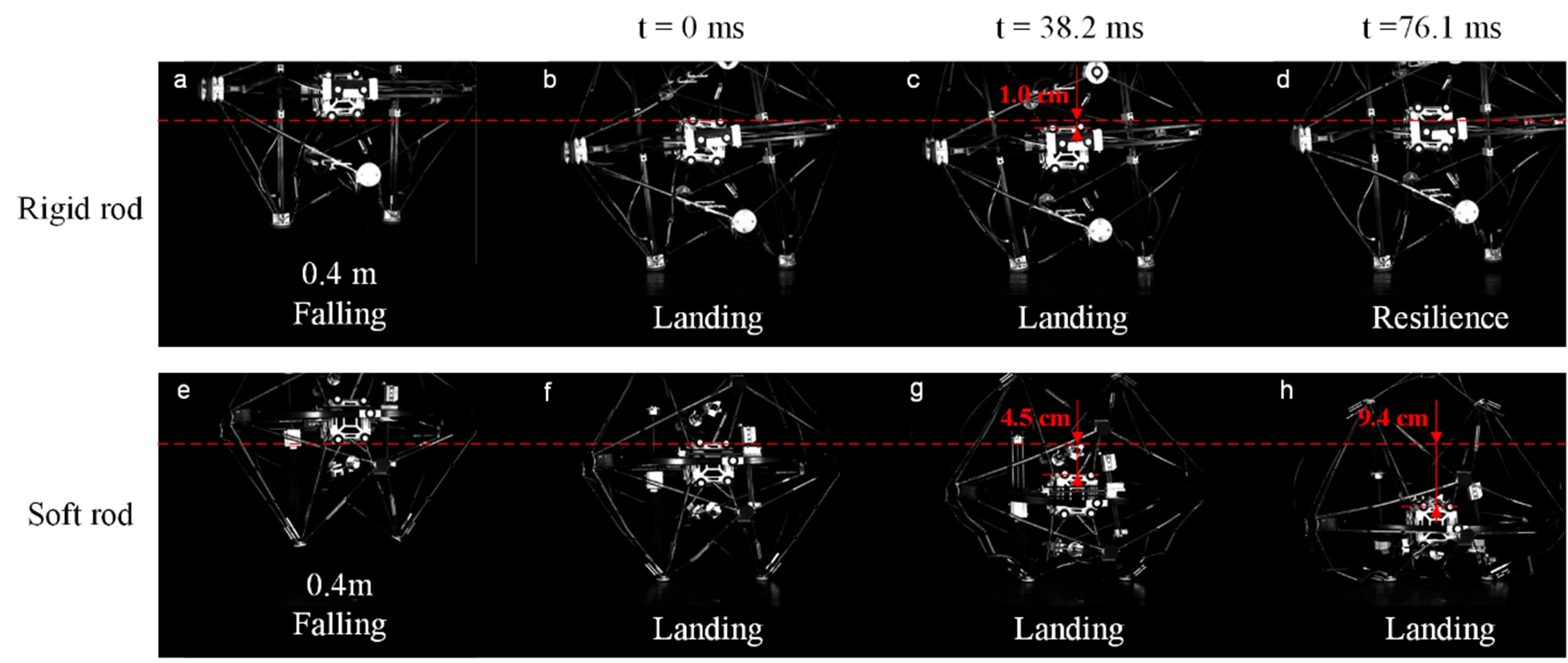
图5.张拉整体机器人跌落实验瞬时摄影
3.拉压不对称特性材料与结构非线性分析的模型简化方法
非光滑拉压非对称本构定律在具有单向接触行为和无拉压结构的生物复合材料结构建模中具有重要应用。基于参数变分原理的二次规划算法在这类问题上具有良好的数值鲁棒性。然而,计算成本的挑战阻碍了它在一些具有大自由度的实际工程结构中的应用。
课题组提出了一种基于扩展多尺度有限元的高效模型简化方法,用于具有拉压非对称特性的复合材料结构的力学分析。在宏观尺度上,构造并求解了一个降阶模型来获得位移场,而在微观尺度上,提出了一个互补有限元公式来获得应力场。为了处理材料非线性,提出了一种桥接上尺度和下尺度计算的两尺度迭代方案。与FEM-PVP相比,所提出的EMsFEM-PVP方法大大节省了计算机的内存和CPU时间。该研究为处理大规模非光滑力学提供了一种广泛适用的数值方法。

图6.具有夹杂物的张拉薄膜式天线
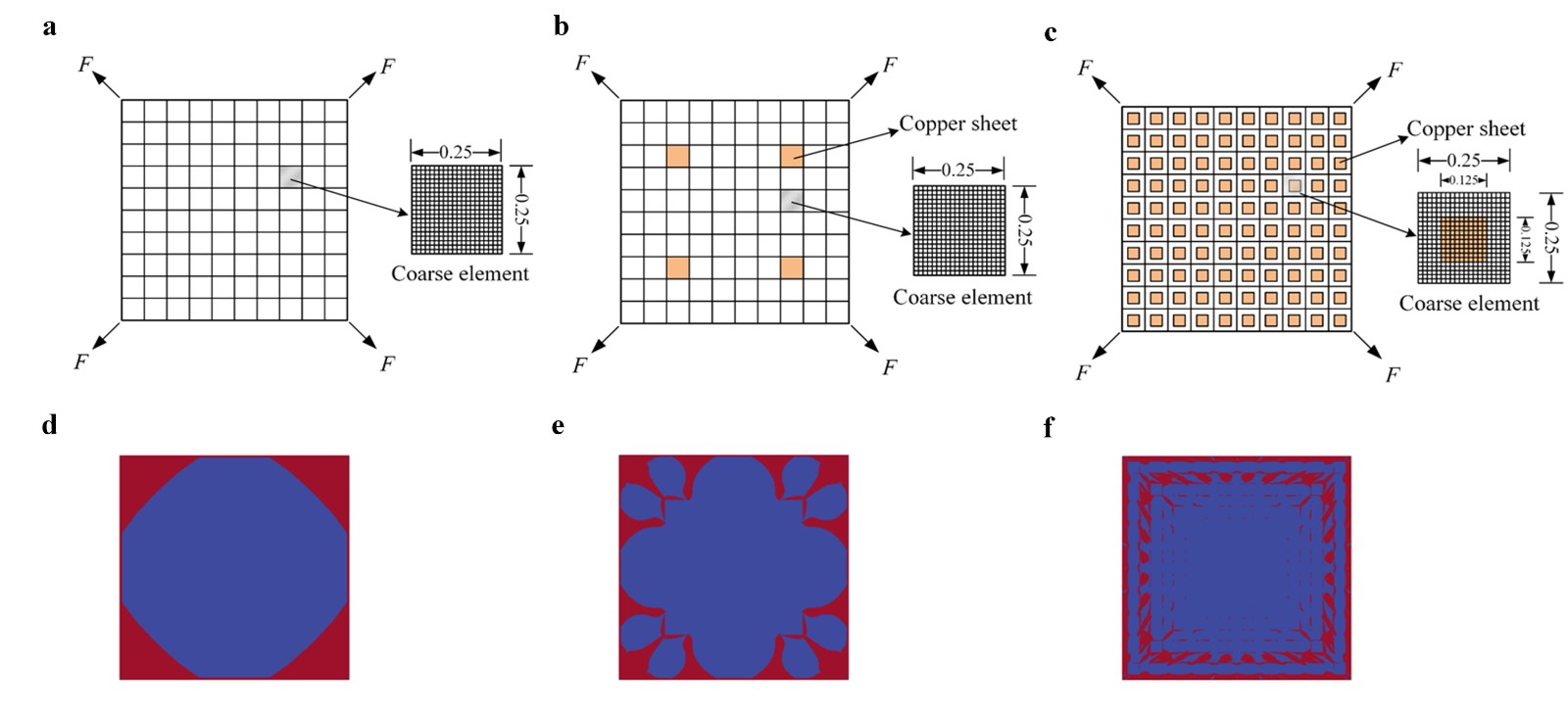
图7.具有不同铜片夹杂物数目的方形膜数值模拟:(a-c)粗网格;(d-f) 褶皱区域。
4. 张拉整体结构大变形分析应用
可展开结构广泛应用于太阳能电池板、充气天线等的支撑结构。传统可展结构存在着复杂的刚性节点和伸缩杆展开等缺陷,解决这些问题的一个可能的方案是基于张拉整体的概念来设计可展开结构。其独特的结构形式也带来了独特的性质,例如强度重量比高、柔性可控、抗冲击性能强等性质。这些性质使其在诸多领域具有应用潜力。
课题组采用参变量共旋算法解决张拉整体结构数值模拟的收敛性问题,将结构大变形分解为结构整体坐标下的刚体位移和单元局部坐标下的小应变变形。算法表现出良好的稳定性,并能准确预测张拉整体结构中松弛绳索的分布情况,可为结构工程师提供可靠的数值参考和指导。该方法被成功地应用到上海航天八院某铰接式伸展机构(图8左)等张拉整体支撑结构的行为预测,数值模拟分析结果受到好评。该方法被进一步应用于空间索网天线结构(图8右)的找形设计。

图8.柔性太阳翼张拉整体支撑结构与模块化索网天线

图9.张拉整体支撑结构变形预测与索网天线单胞找形结果
5. 狭缝空间气氛演化研究
开展装备狭缝内气氛演变建模计算,以此获取狭缝内的气氛演变规律对预测装备老化速率、服役寿命等健康状态信息具有重要意义。装备服役状态演化是一个多物理场耦合、多物理过程交替进行的复杂力学-化学耦合问题。需要考虑在几何模型为亚毫米尺度的狭缝空间,研究包含重力与温度效应、边界化学反应、边界吸释气体、边界渗透泄露、几何模型变化、模型参数变化、初始条件变化等因素下的多组分气氛演化。
为获取狭缝空间气氛长时演化特征,存在着多物理场耦合的复杂流场系统建模困难和时间多尺度下加速计算等问题。课题组基于Maxwell-Stefan模型成功模拟了狭缝空间气体混合物在复杂物理化学边界条件下的扩散演化,并开展了特征时刻下的空间内水汽凝结相变研究计算,完成了对空间内水汽凝结程度和位置的预测。此外,课题组利用动态模态分解DMD等模型降阶加速计算方法,实现了短时内完成对狭缝空间多组分气体在年尺度下的演化预测。
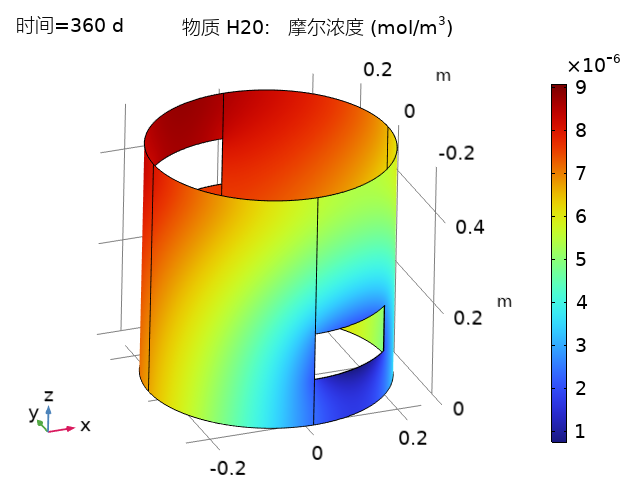
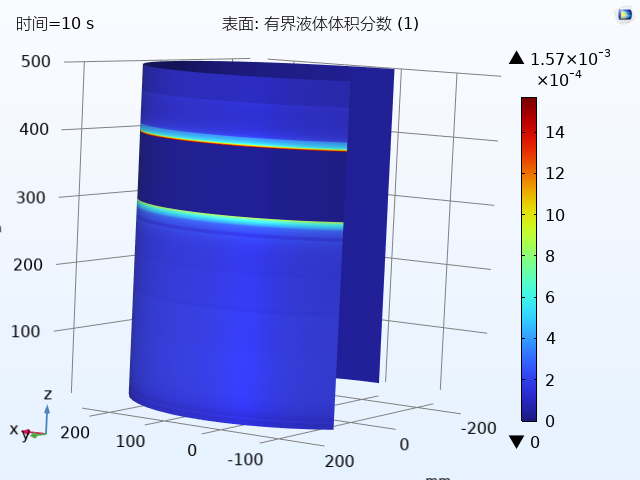
图10.(左)狭缝空间第360天的水蒸气浓度场;(b)狭缝空间在特征时刻下的水气凝结体积分数
10篇代表性论文:
Ge, Y.P., He, Z.G., Li, S.F.,Zhang, L.*, Shi, L.T., 2023. A machine learning-based probabilistic computational framework for uncertainty quantification of actuation of clustered tensegrity structures.ComputationalMechanics. 72(3), 431-450.
Lu, M.K.,Zhang, L.*,Chen, X.J.,Vershinin, A., 2023. A unified variational framework of no-tension and no-compression solids and its application to finite element analysis.InternationalJournal ofSolidsandStructures. 275, 112298.
Zhang, L.*, Lu, M.K., Han, L.L., Cao, J.J., 2021. A model reduction method for nonlinear analysis of materials and structures with tension–compression asymmetric properties.Composite Structures.262, 113613.
Lu, M.K., Zheng, Y.G , Du, J.K.,Zhang, L.*, Zhang, H.W., 2021. An adaptive multiscale finite element method for strain localization analysis with the Cosserat continuum theory.European Journal of Mechanics A-Solids. 92, 104450.
Lu, M.K.,Zhang, L.*, Yan, Z., Wu, J., 2021. Nonlinear analysis of structures made of no-tension/compression materials using an efficient projection-contraction algorithm.Computers & Structures. 224, 106432.
6. Yan, Z.,Zhang, L.*, Jin, W.W., 2020. Improved finite element method for inflated beams with local wrinkles.AIAA Journal. 60(7), 4278-4287.
7. Wu, J.,Zhang, L.*, He, Z.G., Yan, Z., 2020. Comparative analysis of two tensegrity grids considering slack and rupture of cables.AIAA Journal. 58(5), 2321-2329.
8. Lv, J., Zheng, M.H.,Zhang, L.*, Song, C., Zhang, H.W., 2020. Geometrically nonlinear analysis of 3D fluid actuated cellular structures using extended multiscale finite element method.International Journal of Mechanics and Materials in Design. 16(3), 503-517.
9.Zhang, L.*, Dong, K.J., Lu, M.K., Zhang, H.W., 2020. A wrinkling model for pneumatic membranes and the complementarity computational framework.Computational Mechanics. 65(1), 119-134.
10.Zhang, L., Gao, Q., Zhang, H.W.*, 2014. Analysis of 2-D bimodular materials and wrinkled membranes based on the parametric variational principle and co-rotational approach.International Journal for Numerical Methods in Engineering. 98(10), 721-746.
1.串联张拉整体结构大变形分析模拟系统V1.0
2.充气膜结构褶皱变形分析计算模拟系统V1.0
《力学与工程技术的进步(第2版)》第8章:力学与生物医学工程.北京高等教育出版社,2022
1. 国家自然科学基金面上项目:基于贝叶斯推断的充气梁承载极限实时分析方法研究(负责人, 2023~2026, 在研)
2. 重庆交通科研设计研究院科研项目:基于模型和数据的桥梁健康状态评估(负责人, 2023~2024, 在研)
3.中国工程物理研究院重点培育项目:XXXX计算方法(负责人, 2022~2023, 已结题)
4. 国家自然科学基金科技活动专项项目:第六届全国计算力学青年学术研讨会(负责人, 2022,已结题)
5. 重庆市技术创新与应用发展重大主题专项子课题:高可靠性轻型飞机操纵系统研发及应用(负责人, 2019~2022, 已结题)
6. 上海宇航系统工程研究所航天创新基金项目:张拉整体机器人动力学建模分析与模型验证(负责人, 2019~2021, 已结题)
7. 国家自然科学基金面上项目:大型柔性薄膜天线局部褶皱变形的多场多尺度计算方法(负责人, 2019~2022, 已结题)
8.西安交通大学机械结构强度与振动国家重点实验室开放基金项目:张拉整体机器人高效驱动策略研究(负责人, 2018~2020, 已结题)
9.重庆市留学人员回国创业创新支持计划创新类项目:柔性张拉整体结构设计及其应用(负责人, 2019~2021, 已结题)
10. 中央高校基本科研业务费前沿交叉研究专项项目:张拉整体机器人动力学建模及高效驱动策略研究(负责人, 2019~2020, 已结题)
11. 上海宇航系统工程研究所航天创新基金项目:柔性可展结构非线性分析的基础算法及软件开发(负责人, 2017~2019, 已结题)
12. 国家自然科学基金青年基金项目:考虑热力耦合作用的薄膜褶皱分析稳定化算法研究(负责人, 2016~2018, 已结题)
13.中国博士后科学基金第59批面上项目(一等资助):热力耦合作用下薄膜褶皱变形的数值模拟与实验验证(负责人, 2016~2017, 已结题)
14.重庆市基础科学与前沿研究技术专项项目:柔性薄膜褶皱变形的高效数值模拟与实验验证(负责人, 2016~2018, 已结题)
15.中央高校基本科研业务费项目:薄膜在热力耦合载荷作用下的褶皱变形机理研究(负责人, 2015~2017, 已结题)
16.大连理工大学工业装备结构分析国家重点实验室开放基金项目:基于参变量变分原理的薄膜褶皱分析建模与算法研究(负责人, 2014~2016, 已结题)
17.重庆大学引进人才科研启动项目:Tensegrity结构展开过程数值模拟及其高效计算方法(负责人, 2014~2017, 已结题)
18.上海宇航系统工程研究所科研项目:伸展机构非线性计算(负责人, 2016~2017, 已结题)












